ダネットの検定

統計学において、ダネットの検定（ダネットのけんてい、英: Dunnett's test）は、多重比較手順の一つである。カナダの統計学者チャールズ・ダネットによって、多くの処理群のそれぞれと単一の対照群を比較するために開発された。対照群に対する多重比較は多対一（many-to-one）比較とも呼ばれる。

歴史

ダネットの検定は1955年に開発され、臨界値の更新した表が1964年に発表された。

多重比較問題

多重比較、多重性、あるいは多重検定問題は、一組の統計的推定を同時に考える時や、観測値に基づいて選択されたパラメータの一部を推測する時に起こる。多重比較手順の議論における主要問題は、第一種過誤の確率の課題である。様々な方法間での大きな違いは、これらの過誤をいかに制御するかという課題に対して異なるアプローチを取ることから来ている。この問題は部分的には技術的なものである。しかし、どのように誤り率を定義するか、どの程度の最大誤り率を望むのかという、実際にはかなり主観的な問いなのである。ダネットの検定はよく知られており、正規性の仮定が妥当である分布からサンプリングされた全ての処理群を対照群と同時に比較するための多重比較手順において広く使われている。ダネットの検定は、処理群と対照群との多重比較を行った時にファミリーワイズエラー率を${\displaystyle \alpha }$より低く抑えるように設計されている。

ダネットの検定の使用

多重比較問題に関する最初の研究はテューキーとシェッフェによって成された。彼らの手法は、全ての種類の対比較を考慮した一般的なものであった。テューキーの方法とシェッフェの方法は一式の標本平均の間でいくらでも比較をすることができる。一方、ダネットの方法は一つの群とその他の群の比較のみを行うことができる。これによって、対照群と処理群の対比較を行う際の多重比較問題の特別な場合に対処できる。一般に、対比較を行うとすると${\displaystyle {\frac {k(k-1)}{2}}}$回（kは群の数）の比較を行うが、処理群と対照群を比較する場合は${\displaystyle (k-1)}$回の比較のみで済む。もし処理群と対照群の場合により一般的なテューキーやシェッフェの方法を用いると、不必要に広い信頼区間が得られてしまう。ダネットの方法は処理群と対照群の比較の特別な構造を考慮し、より狭い信頼区間を与える。

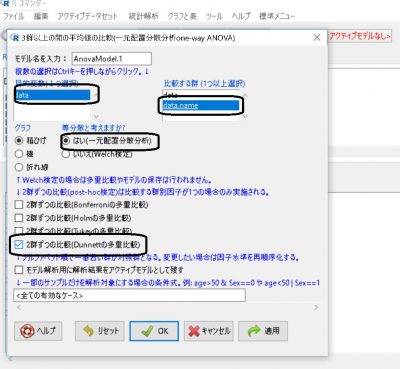
医学的実験ではダネットの検定が非常によく使われる。例えば、3群の動物についての血球数測定を比較する時、1つは対照群、その他2つは2つの異なる薬剤を処理する場合が考えられる。ダネットの検定は農学者にもよく使用される。農学者はある化学物質を土壌に添加した時の作物の収量に与える影響を調べたいので、1つの区画を無処理（対照区画）とし土壌に化学物質を添加した区画（処理区画）と比較する。

ダネットの検定の形式的記述

ダネットの検定は、個々の実験あるいは処理、群についてスチューデントのt-統計量を計算することによって行われる。この統計量によって処理群と単一の対照群を比較する。個々の比較は共通して同じ対照群を持つため、この手順はこれらの比較間に依存性を含有する。具体的には、t-統計量は全て同じ誤差分散の推定量から導かれる。この誤差分散は全ての群（処理群および対照群）にわたる誤差の二乗の和を合併することによって得られる。ダネットの検定での形式的検定統計量は、これらのt-統計量の絶対値の中で最も大きい（両側検定が必要な場合）あるいはt統計量の最も負あるいは最も正のもの（片側検定が必要な場合）である。

ダネットの検定では、共通の臨界値の表を使用できるが、今日はより柔軟な方法がRのような多くの統計パッケージで容易に利用できる。任意のパーセンテージ点に対する臨界値は、片側検定か両側検定かや、比較する群の数、試験の総数に依存する。

仮定

この分析では、実験の結果が数字で表わされ、p 個の処理群と対照群を比較するために実験が行われた場合を考える。結果は一連の観測 ${\displaystyle ({\bar {X_{0}}},...,{\bar {X_{p}}})}$ について計算された (p 1) 個の平均として要約できる。ここで ${\displaystyle ({\bar {X_{1}}},...,{\bar {X_{p}}})}$ は処理された一連の観測、${\displaystyle {\bar {X_{0}}}}$ は対照となる観測、s は p 1 個全ての観察の共通標準偏差の独立した推定値である。p 1 個の観測の全ての ${\displaystyle {\bar {X_{i}}}}$ は独立であり、共通分散 σ² と平均 μ_i を持ち正規分布していると仮定される。また、σ² に対する推定値 s² の存在も仮定される。

計算

ダネットの検定の計算は、${\displaystyle p}$個の差（${\displaystyle {\bar {X_{i}}}-{\bar {X_{0}}}}$、したがって処理群の平均と対照群の平均の差）の真の値あるいは期待値に関する信頼記述の計算に基づく手順である。この手順によって、${\displaystyle p}$個全ての記述${\displaystyle {\bar {X_{i}}}-{\bar {X_{0}}}}$が同時に正しい確率が指定された値${\displaystyle P}$と等しくなる。処理群の平均と対照群の平均との間の差の真の値に関する片側上方（あるいは下方）信頼区間を計算する時、${\displaystyle P}$はこの実際の値が信頼区間の上方限界よりも小さい（あるいは下方限界よりも大きい）確率を表わす。両側信頼区間を計算する時、${\displaystyle P}$は真の値が上方限界と下方限界の間にある確率を表わす。

はじめに、利用できるN個の観測を${\displaystyle X_{ij}}$（${\displaystyle i=1...p}$、${\displaystyle j=1...N_{i}}$）によって示し、共通分散を例えば${\displaystyle s^{2}={\frac {\sum _{i=0}^{p}\sum _{j=1}^{N_{i}}(X_{ij}-{\bar {X_{i}}})}{n}}}$によって推定する（${\displaystyle {\bar {X_{i}}}}$は群${\displaystyle i}$の平均、${\displaystyle N_{i}}$は群${\displaystyle i}$の観測の数、自由度${\displaystyle n=\sum _{i=0}^{p}N_{i}-(p 1)}$）。上述したようにここでは、${\displaystyle p}$個全ての信頼区間が対応する${\displaystyle m_{i}-m_{0}}$を含む確率が${\displaystyle P}$と等しくなるように、個々の差${\displaystyle m_{i}-m_{0},(i=1...p)}$について独立した信頼限界を得たい。

ここで、${\displaystyle p}$個の処理群と1個の対照群がある一般的な場合を考えると、

${\displaystyle z_{i}={\cfrac {{\bar {X_{i}}}-{\bar {X_{0}}}-(m_{i}-m_{0})}{\sqrt {{\cfrac {1}{N_{i}}} {\cfrac {1}{N_{0}}}}}}}$

${\displaystyle D_{i}={\cfrac {{\bar {X_{i}}}-{\bar {X_{0}}}-(m_{i}-m_{0})}{s{\sqrt {{\cfrac {1}{N_{i}}} {\cfrac {1}{N_{0}}}}}}}}$

と書ける。${\displaystyle D_{i}={\frac {z_{i}}{s}}}$とも書くことができ、これは自由度nのスチューデントのt分布に従う。${\displaystyle p}$個の処理効果${\displaystyle m_{i}-m_{0},(i=1...p)}$に対する共有の信頼係数${\displaystyle P}$下方信頼限界は以下の式で表わされ、

${\displaystyle {\bar {X_{i}}}-{\bar {X_{0}}}-d_{i}'s{\sqrt {{\frac {1}{N_{i}}} {\frac {1}{N_{0}}}}},i=1...p}$

${\displaystyle p}$個の係数${\displaystyle d_{i}'}$は${\displaystyle Prob(t_{1}$となるように選ばれる。

同様に、上方限界は以下の式で表わされる。

${\displaystyle {\bar {X_{i}}}-{\bar {X_{0}}} d_{i}'s{\sqrt {{\frac {1}{N_{i}}} {\frac {1}{N_{0}}}}},i=1...p}$

したがって、上方と下方を併せると信頼区間は

${\displaystyle {\bar {X_{i}}}-{\bar {X_{0}}}\pm d_{i}'s{\sqrt {{\frac {1}{N_{i}}} {\frac {1}{N_{0}}}}},i=1...p}$

となる（${\displaystyle d_{i}''}$は${\displaystyle Prob(|t_{1}|$を満たすように選ばれる）。両側検定での${\displaystyle d_{i}''}$、片側検定での${\displaystyle d_{i}'}$の具体的な値の解は表で与えられている。この臨界値の表は1964年に更新されている。

例

布の破壊強度

データは、標準製法および異なる3種類の化学プロセスによって処理された布の破壊強度の測定値を表わしている。

ここで、p = 3、N = 3である。平均分散は${\displaystyle s^{2}=19}$であり、これは自由度 (p 1)(N-1)=8 の4組の共通分散の推定値である。

平均分散は以下のように計算できる。

${\displaystyle {\frac {55^{2} 47^{2} 48^{2} 55^{2} ... 41^{2}-3(50^{2} 61^{2} 52^{2} 45^{2})}{8}}={\frac {152}{8}}=19}$.

標準偏差は${\displaystyle s={\sqrt {19}}=4.36}$、2つの平均間の差の推定標準誤差は${\displaystyle s{\sqrt {\frac {2}{N}}}=4.36{\sqrt {\frac {2}{N}}}=3.56}$である。信頼限界を与えるために、観測された平均間の差に加えるあるいは差し引かなければならない量はテューキーによって「allowance（許容量）」と呼ばれており、式${\displaystyle A=t_{s}{\sqrt {\frac {2}{N}}}}$で与えられる。値tは片側検定の場合はダネットの表1から、両側検定の場合はダネットの表2から得られる。p = 3、自由度 = 8の場合、p=95%でのt値は、片側検定では t = 2.42、両側検定では t = 2.88である。片側検定の場合、「許容量」はA=(2.42)(3.56)=9であり、実験者は以下のように結論できる。

• プロセス1を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 61-50-9=2lbs}$上回る。
• プロセス2を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 52-50-9=-7lbs}$上回る。
• プロセス3を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 45-50-9=-14lbs}$上回る。

上記の3つの結論が統合された記述は95%の信頼係数を持つ。すなわち、長期的には、このような統合された記述の95%が実際に正しい。これらの差に対する上方限界は類似したやり方で得ることができる。両側限界では、許容量はA=(2.94)(3.56)=11であり、実験者は以下のように結論できる。

• プロセス1を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 61-50-11=0lbs}$と${\displaystyle 61-50 11=22lbs}$の間の量だけ超える。
• プロセス2を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 52-50-11=-9lbs}$と${\displaystyle 52-50 11=13lbs}$の間の量だけ超える。
• プロセス3を用いた破壊強度は標準製法によるものを少なくとも${\displaystyle 45-50-11=-16lbs}$と${\displaystyle 45-50 11=6lbs}$の間の量だけ超える。

これら3つの記述に対する統合された信頼係数は95%を超える。

脚注